
However, if you have messy x-intercepts (as in the example above) or if the quadratic doesn't actually cross the x-axis (as you'll see on the next page), then you'll need to use the formula to find the vertex. So you can just average the two intercepts to get the location of the axis of symmetry and the x-coordinate of the vertex. Helpful note: If your quadratic's x-intercepts happen to be nice neat numbers (so they're relatively easy to work with), a shortcut for finding the axis of symmetry is to note that this axis, this vertical line, is always exactly between the two x-intercepts. So in the example above, then the axis would be the vertical line x = h = −1/6. If you're asked for the axis, write down the line " x = h", where h is just the x-coordinate of the vertex. This vertical line, right through the vertex, is called the axis of symmetry.
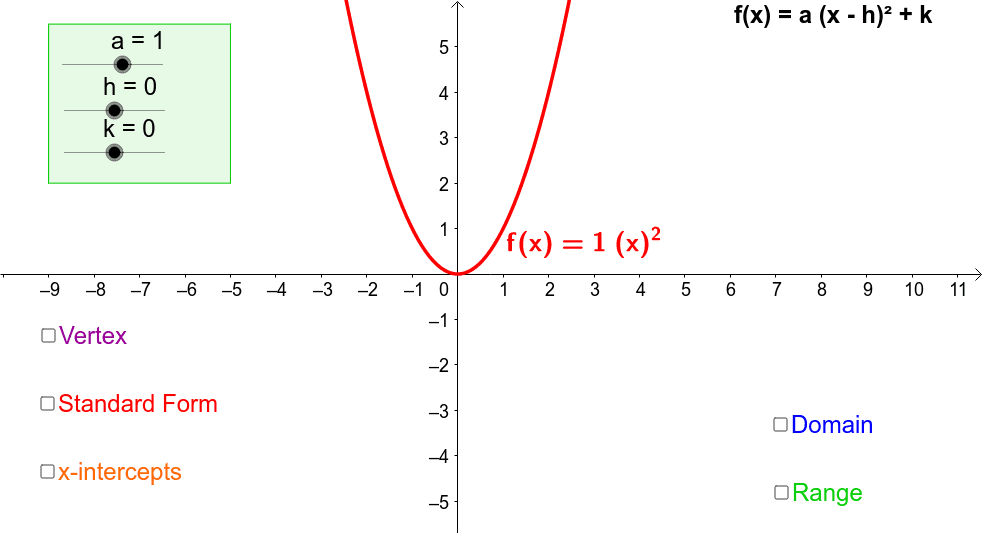

If you look at a parabola, you'll notice that you could draw a vertical line right up through the middle which would split the parabola into two mirrored halves. Since the vertex is a useful point, and since you can "read off" the coordinates for the vertex from the vertex form of the quadratic, you can see where the vertex form of the quadratic can be helpful, especially if the vertex isn't one of your T-chart values. (Note: The " a" in the vertex form " y = a( x − h) 2 + k" of the quadratic is the same as the " a" in the common form of the quadratic equation, " y = ax 2 + bx + c".) The same reasoning works, with k being the largest value and the squared part always subtracting from it, for upside-down parabolas. And the squared part is zero when x − h = 0, or when x = h. So the smallest y can possibly be is y = k, and this smallest value will happen when the squared part, x − h, equals zero. So you'll always have that fixed value k, and then you'll always be adding something to it to make y bigger, unless of course the squared part is zero. The squared part of y = a( x − h) 2 + k is always positive (for a right-side-up parabola), unless it's zero.

On the same grid, she graphs the functiong (x) (x + 6)2 - 3. Justine graphs the function f (x) (x - 7)2 - 1. The graph of the function is 1 unit up and 2 units to the left from the graph of y x2. If the quadratic is written in the form y = a( x − h) 2 + k, then the vertex is the point ( h, k). The range is all real numbers greater than or equal to 1. This point, where the parabola changes direction, is called the "vertex". Parabolas always have a lowest point (or a highest point, if the parabola is upside-down). In order to find the vertex from this form, you must first find the x-coordinate of the vertex which is x - b/2a.


 0 kommentar(er)
0 kommentar(er)
